"Deine neue HiFi-Anlage ist ein echt super tolles Teil. Sie bringt
dich so richtig in Fahrt.
Sie kostet zwar 1000 €, aber ein Ratenkauf mit 12 Raten zu 100 €
monatlich machts möglich. Der Verkäufer meint: ""12
% Zinsen für einen Kredit sind üblich und eigentlich ist das
alles schon fast geschenkt.""."
Aufgabe 1:
Bewerte bitte in Ruhe und wohl überlegt die Aussagen des Verkäufers!
Lösung:
12 Raten je 100 € ergeben einen Gesamtbetrag von 1.200 €.
Das sind 200 € mehr als der eigentliche Kaufpreis.
Der Preis für die Anlage ist um 20% höher als der Barpreis der
Anlage von 1.000 €.
Da die Rückzahlung aber sofort beginnt, ist der Kreditzinssatz jedoch
höher.
Wir berechnen den monatlichen Restbetrag unseres Kredites jetzt mit dem
jährlichen Zinssatz von 12%, also 1% monatlich. Dabei rechnen wir
die einzelnen Rechenschritt weiter nicht aus, um den mathematischen Zusammenhang
erkennen zu können.
1. Monat : (1000-100)*1.01
2. Monat : ((1000-100)*1.01-100)*1.01
= (1000*1,01-100*1,01-100)*1,01
= 1000*1,012
- 100*1,012 - 100*1,01
3. Monat : ((1000*1,012
- 100*1,012 - 100*1,01) - 100)*1,01
= 1000*1,013
- 100*1,013 - 100*1,012 - 100*1,01
4. Monat : ((1000*1,013
- 100*1,013 - 100*1,012 - 100*1,01 - 100)*1,01
= 1000*1,014
- 100*1,014 - 100*1,013 - 100*1,012 -
100*1,01
...
12. Monat :
((1000*1,0111 - 100*1,0111
- 100*1,0110 - 100*1,012 - 100*1,01 -100)*1,01
= 1000*1,0112
- 100*1,0112 - 100*1,0111 ... -100*1,012
- 100*1,01
= 1000*1,0112 - 100 * ( 1,0112 + 1,0111
... + 1,012 + 1,01 )
allgemein: für n Raten:
1000*1,01n
- 100*1,01n- 100*1,01n-1 ... -100*1,012
- 100*1,01
= 1000*1,01n -
100*(1,01n + 1,01n-1 ... + 1,012 + 1,01)
Allgemein gilt also;
= BW * (1+ZS)ZZR
- RMZ*(
(1+ZS)ZZR+ (1+ZS)ZZR-1 ... + (1+SZ)12
+ ZS )
wobei BW der Barwert (der Kreditbetrag), ZS
der für den Zahlungszeitraum ZZR gültige
Zinssatz und RMZ der Betrag der regelmäßigen
Zahlung ist.
Die allgemeine Beziehung zwischen unseren Größen ist damit:
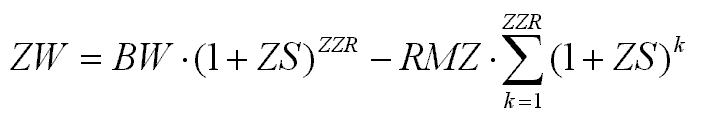
Zur Absicherung dieser Beziehung verwende Kreditformel.xls
bzw. die DERIVE-Datei kredit-drw .
Diese Gleichung kann ohne Schwierigkeiten zur Berechnung von ZW, BW bzw.
RMZ herangezogen werden.
Eine Auflösung nach ZS oder ZZR ist nicht leicht möglich.
Im Abschnitt Finanzmathematische EXCEL-Funktionen lernen wir mehr
über diese Probleme und deren Lösung.
Wenden wir unser Wissen über die harmonischen Reihe
![]()
und deren Teilsumme (Partialsumme)
![]()
an, so erhalten wir unter Verwendung q = (1+ZS)